Introduction – What is the Blockchain?
 In the world of cryptocurrencies, the ‘blockchain’, concept is the simplest topic to begin with, before venturing into the more complicated areas of cryptocurrencies (also called tokens in some contexts) and mining. A blockchain is a distributed database that contains a continuously growing list of ordered records that are grouped together in ‘blocks’. Instead of the database being stored on one server, the database is replicated and synchronized across multiple machines (servers, laptops, etc.), commonly referred to as nodes, that are distributed across a network. Blockchains fall into a category of technology referred to as distributed ledger technology (DLT).
In the world of cryptocurrencies, the ‘blockchain’, concept is the simplest topic to begin with, before venturing into the more complicated areas of cryptocurrencies (also called tokens in some contexts) and mining. A blockchain is a distributed database that contains a continuously growing list of ordered records that are grouped together in ‘blocks’. Instead of the database being stored on one server, the database is replicated and synchronized across multiple machines (servers, laptops, etc.), commonly referred to as nodes, that are distributed across a network. Blockchains fall into a category of technology referred to as distributed ledger technology (DLT).
In addition to the database being distributed across a network, the data is also stored in blocks (groups of records), where each block is tied or chained to the previous block in such a way that it is not possible to alter the data in one block without affecting the data in subsequent blocks. The term ‘blockchain’ is therefore derived from the fact that transactions or records are grouped into blocks, and each block is linked or chained to the previous one. But the blocks are cleverly chained together, using cryptographic hash functions.
Enter Cryptography…
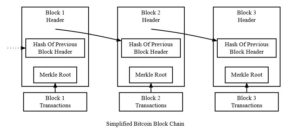
Each block of transactions in a blockchain typically contains not only the list of transactions, but other bits of data such as a block header, the block size and a time stamp, to name a few. Usually, the block header will contain cryptographic hashes of the transaction data in that block, as well as a cryptographic hash of the previous block’s header. This is illustrated very simplistically below:
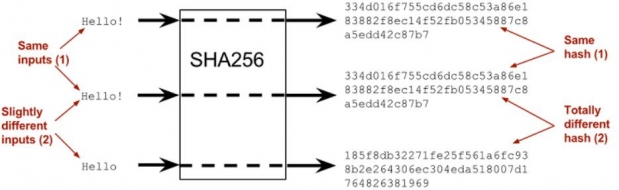
Hash functions are one-way mathematical functions that can take any arbitrary data as input and create an output of fixed length. This output is usually referred to as a hash value, or simply a hash. It is a one-way function because it is trivial to compute the hash output using data as an input. However, you cannot calculate the original input using the hash output. One of hash algorithms employed in Bitcoin for example is the SHA256 (Simple Hashing Algorithm) function.
The tiniest of changes to any of the data used as input to SHA256 would cause the hash output to be different. Therefore, because a blockchain’s header contains the hash of the previous block’s header, any alteration to a block’s data would result in a change to the hash of the subsequent block, and so on. The diagrams below illustrate how SHA256 functions, and how hashes are used to chain blocks together:
This cryptographic linking of the blocks is frequently what is thought to give the blockchain its immutability and security. This is a misconception. The real immutability of the blockchain comes from the distribution and decentralisation of the mining power of the nodes on the network and the manner in which they reach consensus for how records are added to the database. So what is mining?
Before moving onto mining, this video below is a fun but accurate take on this misconception of the ‘blockchain’ being the disruptive force many are touting it to be. It also alludes to the importance of decentralisation in the entire context.
So what is mining?
Mining is very simply the process of grouping transactions into a block, and then mining for a specific number, such that when this number is added to the block header’s data, the resulting hash of that header is a value that meets certain requirements, as agreed to by the participants of the cryptocurrency network.
This number cannot be calculated because of the fact that hash functions are one-way functions. Instead, computers have to mine through billions or even trillions of numbers to find one that will make the block header’s hash meet the requirement. In the case of Bitcoin, the requirement is that the hash is less than a stipulated target.
Basically, a miner’s computer generates hashes at a rate of megahashes per second (MH/s), gigahashes per second (GH/s), or even terahashes per second (TH/s) (depending on processing power of the computer), guessing all possible 64-digit numbers until they arrive at a solution. In other words, it’s a gamble.
Once a miner finds this number, his/her block is very easily validated by the rest of the network by simply running that block through the hash function. If the block is validated, it is successfully added to the blockchain and all nodes update their local blockchains accordingly. In return for finding a valid block, a miner is rewarded with cryptocurrency.
Why does mining make everything work?
If transactions on the bitcoin network were simply grouped into blocks and linked via the hashes of their block headers, the only thing it really achieves is the cryptographic linking of the blocks. This is trivial and rather pointless. Any participant with the most computing power would be able to create blocks of transactions faster than others, and create a record of transactions that may defraud others.
The process of mining creates the equivalent of a competitive lottery that prevents any individual or group from continuously adding consecutive blocks to the blockchain. In this way, no group or individual can control what is included in the blockchain or replace parts of the blockchain to roll back their own spends. The process of mining deliberately makes it difficult for anyone to create a valid block, i.e. a block with the right hash value.
Because the blocks are linked or chained together, it is impossible to modify the contents of one block with modifying all subsequent blocks. The cost of tampering with a particular block increases with every new block added to the blockchain. It requires (on average) as much hashing power to propagate a modified block as what the entire Bitcoin network expended between the time the original block was created and the present time. Only if you acquired a majority of the network’s hashing power, could you reliably execute such a “51 percent attack” against transaction history. Although, even with less than 50% of the hashing power, one still has a good chance of performing such attacks. This is why decentralisation of mining power is what creates the immutability of the blockchain, not the cryptographic chaining of the blocks.
Mining and specific consensus rules enforces the neutrality of the network, and allows different computers to agree on the state of the system. These rules prevent previous blocks from being modified because doing so would invalidate all the subsequent blocks.
The unique hash that miners have to find is also called a “proof of work” number. It represents proof the computing work was done to create a valid block.
Closing comments
For a block to be added to the blockchain, the majority of nodes must first reach consensus. In Bitcoin, consensus is reached through a process called ‘Proof of work’ (more on this later), while Ethereum currently seeks to use Proof of Stake as its consensus mechanism.
If you look at the Bitcoin blockchain, you will see each and every single transaction since the beginning of 2009. Each of the thousands of nodes hold the same sets of records. This makes it impractical to alter transaction history, because you would have to gain control over the majority of the computers before you can change the agreed-upon truth that the entire network of nodes reached consensus on.
In a traditional database, one can perform four functions on the data: Create, Read, Update, and Delete (collectively known as the CRUD commands). The blockchain is designed to be an append-only structure. Nodes can only add more data, in the form of additional blocks. All previous data is permanently stored and cannot be altered. Therefore, the only operations associated with blockchains are:
- Read operations: these query and retrieve data from the blockchain
- Write operations: these add more data onto the blockchain
Decentralized validation of records eliminates the risks of centralized control. Anyone with sufficient access to a centralized database can destroy or corrupt the data within it. Users of a centralised database are therefore reliant on the security infrastructure, integrity of the database administrator, and so forth.