“Bitcoin is more than just money. It is a sophisticated and revolutionary way of ensuring trust in the system, without needing any participant to be trusted.“
Imagine you are the general of an army for the Byzantine Empire. You and a general of another Byzantine army decide to attack an enemy city. Both your armies approach the city from opposite sides and set up camp. The two of you need to agree on an exact time to simultaneously attack because the city will be able to withstand the attack from only one army.
Your armies share a messenger who you use to communicate with one another in order to decide on a time to attack. The messenger needs to get from one army’s camp to the other either through or around the enemy city. The problem is that the messenger (or the other general for that matter) may not be trustworthy and there is therefore no way of knowing whether the message that one army received from the other is authentic. If the messenger is compromised by the enemy, or if the messenger is a traitor or if the message is intercepted and changed before reaching the other general, it will result in your armies attacking at different times, or possibly in only one army attacking. There is no way to guarantee the requirement that each general is certain that the other has agreed to the attack plan. Both of you will always be left wondering whether your last messenger got through. This Two Generals Problem has been proven to be unsolvable.
This is in effect, the Byzantine General’s Problem. Somehow, the generals need to reach an agreement on the attack time. This agreement is called consensus.
Now even if the first message goes through, the second general has to acknowledge that he received the message, so he sends the messenger back to the first general, thus repeating the previous risk where the messenger can get caught or bribed to send a false acknowledgement. Imagine that there are many armies with generals surrounding the city, and the city can withstand an attack from say half of the armies. The situation now becomes immensely complicated. We now need to reach consensus on the plan of attack, not just between 2 armies, but between many armies. So what is the solution? And how does this relate to Bitcoin and its blockchain?
How do we solve this problem? How does it relate to Bitcoin?
Well, in trying to create a ‘trustless’ peer-to-peer electronic payment solution, a similar problem needed to be solved. Since there is no central authority to rely on to confirm the validity of the transactions between parties, and because the transactions are being executed on a network where there are potential bad actors (like the treacherous generals and the enemy city) who could divert money to themselves, a mechanism was needed for parties to a transaction to agree on the validity of the payment details (analogous to the messages between the generals). Furthermore, the solution needed to work without network participants being able to trust or know each other or any other network participants. Bitcoin solved this problem!
“For solving this Byzantine Generals Problem, Bitcoin (and now incorrectly, the blockchain) has been touted as one of the greatest inventions in Computer Science since the internet.”
For solving this Byzantine Generals Problem, Bitcoin (and now incorrectly, the blockchain) has been touted as one of the greatest inventions in Computer Science since the internet. Bitcoin provided a way to reach consensus in a distributed system. Bitcoin is more than just money. It is a sophisticated and revolutionary way of ensuring trust in the system, without needing any participant to be trusted.
How was this achieved?
Encrypting the message
Let’s relate the Byzantine Generals Problem to payment transactions on a network, by first examining the messages between the generals themselves. And for fun, let’s imagine that our generals have modern-day computers. The messages between the generals can be thought of as plain text being sent over an electronic network. This is a problem because plain text is easily manipulated. The first part of the solution lies in finding a way to ensure that the message itself has not been tampered with. Fortunately, this is easy. We can make use of a mathematical tool called a hash function.
A hash function is able to take input data, whether it is the plain text messages between our fictitious generals or more complex payment transactions, and produce a unique output string of fixed length. A hash function is a one-way function, meaning that you can determine the output hash by using the input data, but you cannot use the output hash to determine the original input data. Stated differently, the hash cannot be decrypted to reproduce the original input data.
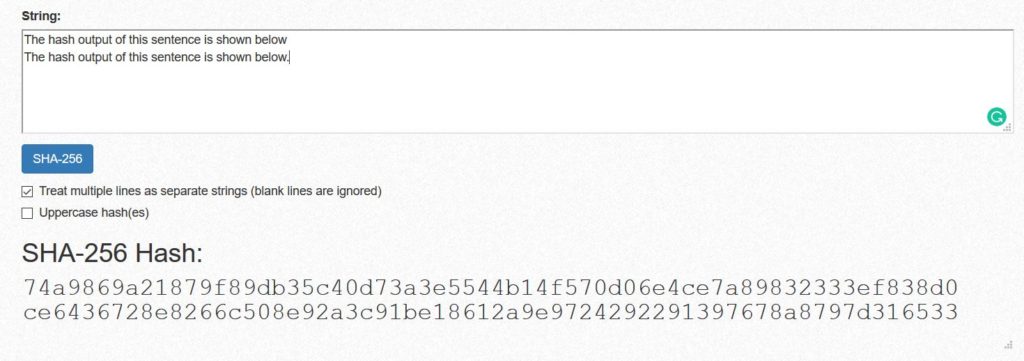
A slight change to the input data would result in a different, but still unique hash. In this illustration, only a full-stop added at the end of the sentence completely changed the hash output.
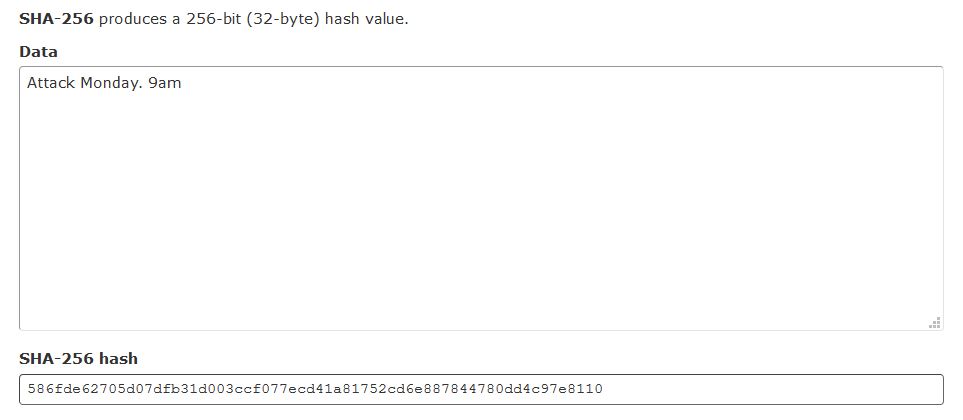
Let’s take a look at an example. Suppose the message that General 1 wants to send is “Attack Monday. 9am”. He would then calculate the hash (using a fictitious computer) and the result would look something like this:
Note the hexadecimal format (586FDE62705D07DFB31D003CCF077ECD41A81752CD6E887844780DD4C97E8110). General 2 would receive this message, and confirm (using his computer) that the hash matches the attack instruction. So now, we’ve accomplished the task of ‘securing’ the original text message. However, what if the city also has computing power? And what if in the more realistic scenario, there are multiple generals surrounding the city? Or in our modern terms, multiple network participants?
The city would be able to use its own computers to intercept the original message, amend it, create its new hash, and forward this on to the other generals. If the city had superior computing power, and/or had more spies, and/or had treacherous generals colluding with it, it would more easily be able to amend, hash and forward the fraudulent message on to more generals before they receive the original message. The generals would still confirm that the fraudulent message is authentic, but it would be the wrong message! And if the city had today’s computing power, running a hash function is trivial and very fast. So now what? Going beyond encryption to Proof of Work